Sitting Arrangement Problems

Problem Description

Sitting Arrangement Problems constitute a comprehensive family of NP-hard combinatorial optimization problems that involve optimally assigning agents (people, resources, or entities) to positions in various graph structures based on their preferences or relationships. These problems arise in diverse contexts ranging from social optimization to resource allocation and scheduling.

The core challenge involves finding arrangements that:

• Maximize overall satisfaction by placing positively-related agents close together
• Minimize conflicts by separating negatively-related agents
• Satisfy structural constraints imposed by the underlying graph topology
• Optimize various objective functions such as sum of utilities, minimum utility, or stability criteria

Problem Variants

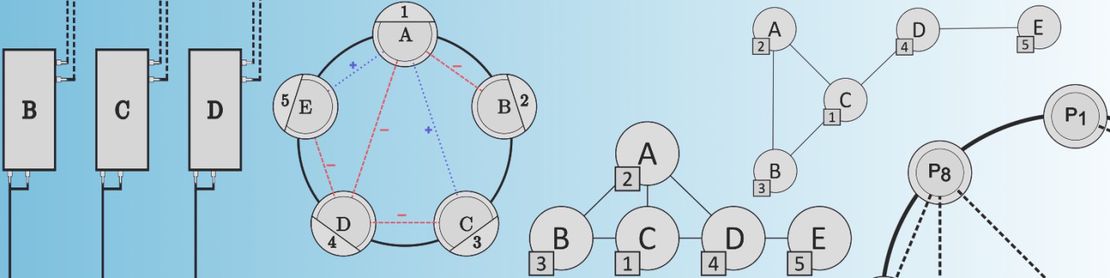
1. Cyclic Minimum Sitting Arrangement Problem

The most studied variant involves embedding a signed input graph into a cycle host graph, where:

• Positive edges represent favorable relationships (should be close)
• Negative edges represent conflicts or unfavorable relationships (should be separated)
• The objective is to minimize the total cost of the arrangement

2. Linear Sitting Arrangement Problem

Agents are arranged in a linear sequence (path graph) rather than a cycle, often appearing in:

• Conference seating optimization
• Production line worker assignment
• Sequential scheduling problems

3. Hedonic Seat Arrangement Problems

Four main optimization criteria:

• Maximum Welfare Arrangement (MWA): Maximizing sum of all agents’ utilities
• Maximin Utility Arrangement (MUA): Maximizing the minimum utility among agents
• Stable Arrangement (STA): Finding arrangements where no agent wants to swap positions
• Envy-free Arrangement (EFA): Ensuring no agent prefers another’s position

4. Multi-Table Arrangement Problems

Extension to multiple tables or groups with additional constraints:

• Oberwolfach Problem: Scheduling multiple seating rounds with no repeated pairings
• Tournament Scheduling: Ensuring balanced interaction patterns
• Conference Organization: Optimizing networking opportunities

Mathematical Formulation

Given a signed graph G = (V, E, w) where:

• V = set of n agents
• E = set of relationships between agents
• w: E → ℝ = weight function (positive for attraction, negative for repulsion)

Find an arrangement π: V → {1, 2, …, n} that minimizes:

$$\sum_{(u,v) \in E} w(u,v) \cdot d_H(\pi(u), \pi(v))$$

where d_H represents the distance in the host graph H (cycle, path, or other structure).

Computational Complexity

• General Problem: NP-hard for most variants and graph classes
• Special Cases: Some polynomial-time solvable instances exist for specific graph structures:
  • Stars and paths with certain preference patterns
  • Matchings with symmetric preferences
  • Trees with monotonic utility functions

The complexity varies significantly based on:

• Graph topology (cycle vs. path vs. general graphs)
• Preference structure (symmetric vs. asymmetric, cardinal vs. ordinal)
• Objective function (sum vs. min vs. stability criteria)

Solution Approaches

Exact Methods

• Integer Linear Programming (ILP) formulations
• Branch-and-bound algorithms for small instances
• Dynamic programming for specific graph classes

Heuristic and Metaheuristic Methods

• Multi-Armed Bandit approaches combining constructive heuristics with local search
• Variable Neighborhood Search (VNS) for local optimization
• GRASP (Greedy Randomized Adaptive Search Procedures)
• Genetic algorithms with specialized crossover operators
• Simulated annealing with problem-specific neighborhood structures

Hybrid Approaches

• Multi-Armed Bandit + VNS: Combining exploration-exploitation strategies with local improvement
• Construction + Local Search: Greedy-randomized construction followed by variable neighborhood descent
• Machine Learning-guided heuristics: Using learned patterns to guide search

Applications

Social and Organizational

• Conference and event planning: Optimizing networking opportunities
• Team formation: Balancing personalities and expertise
• Classroom seating: Considering student interactions and learning objectives
• Restaurant table assignment: Maximizing customer satisfaction

Industrial and Operational

• Production line optimization: Worker placement considering collaboration and conflicts
• Shift scheduling: Balancing team dynamics across work periods
• Resource allocation: Placing resources to minimize interference and maximize cooperation

Computational and Algorithmic

• Network design: Node placement in communication networks
• VLSI design: Component placement considering signal interference
• Distributed computing: Task allocation considering communication costs

Related Publications

The Multi-armed bandit for the cyclic minimum sitting arrangement problem represents a significant advancement in this field, demonstrating how modern optimization techniques can effectively tackle these challenging problems. This work establishes new state-of-the-art results for cyclic arrangements on signed graphs.

Other relevant research includes:

• Optimal seat arrangement complexity analysis
• Hedonic game theory applications
• Graph bandwidth and arrangement problems
• Signed graph embedding techniques

Research Directions

Theoretical Advances

• Approximation algorithms with better performance guarantees
• Parameterized complexity analysis for various problem parameters
• Online variants where agents arrive dynamically

Algorithmic Improvements

• Machine learning integration for pattern recognition in preferences
• Parallel and distributed algorithms for large-scale instances
• Robust optimization handling uncertain preferences

Application Extensions

• Multi-objective optimization balancing competing criteria
• Dynamic arrangements adapting to changing preferences over time
• Fairness considerations ensuring equitable treatment across agent groups

References

1. Robles, M., Cavero, S., Pardo, E. G., & Cordón, O. (2025). Multi-armed bandit for the cyclic minimum sitting arrangement problem. Computers & Operations Research, 179, 107034.

2. Aziz, H., Brandl, F., Brandt, F., & Harrenstein, P. (2019). Hedonic Games. Handbook of Computational Social Choice, Cambridge University Press.

3. Even, S., & Shiloach, Y. (1975). NP-completeness of several arrangement problems. Technical Report, Technion, Israel Institute of Technology.

4. Garey, M. R., & Johnson, D. S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman and Company.

Acknowledgments

This problem family overview is part of the RedHEUR4.0 initiative, highlighting the importance of graph-theoretic optimization problems in modern computational challenges. The development of efficient algorithms for sitting arrangement problems contributes to advances in social optimization, resource allocation, and combinatorial optimization theory.