Graph domination

Problem Description

Graph Domination problems constitute one of the most active and versatile areas within graph theory, with a wide range of applications across various disciplines. This family of problems is based on the general idea of selecting a subset of vertices that exerts some form of control or coverage over the rest of the graph, while considering different structural, operational, or cost-related constraints. This subset of nodes is referred to as a Dominating Set.

Industrial Context

This family of problems have strong practical motivation. For example, they arise naturally in the design and operation of communication networks, where it is necessary to place control, relay, or monitoring nodes in such a way that the entire network is adequately covered. They are also useful for locating sensors in wireless networks, in the planning of public services (such as emergency stations, logistics centers, or distribution points), and in the spread of information or influence in social networks.

In the context of influence in social networks, various authors have addressed influence maximization problems, whose goal is to identify the smallest set of users capable of influencing the rest of the network through their connections. This goal is directly related to the search for dominating sets, as these allow reaching all users using a one-step cascade diffusion model.

Common Challenges

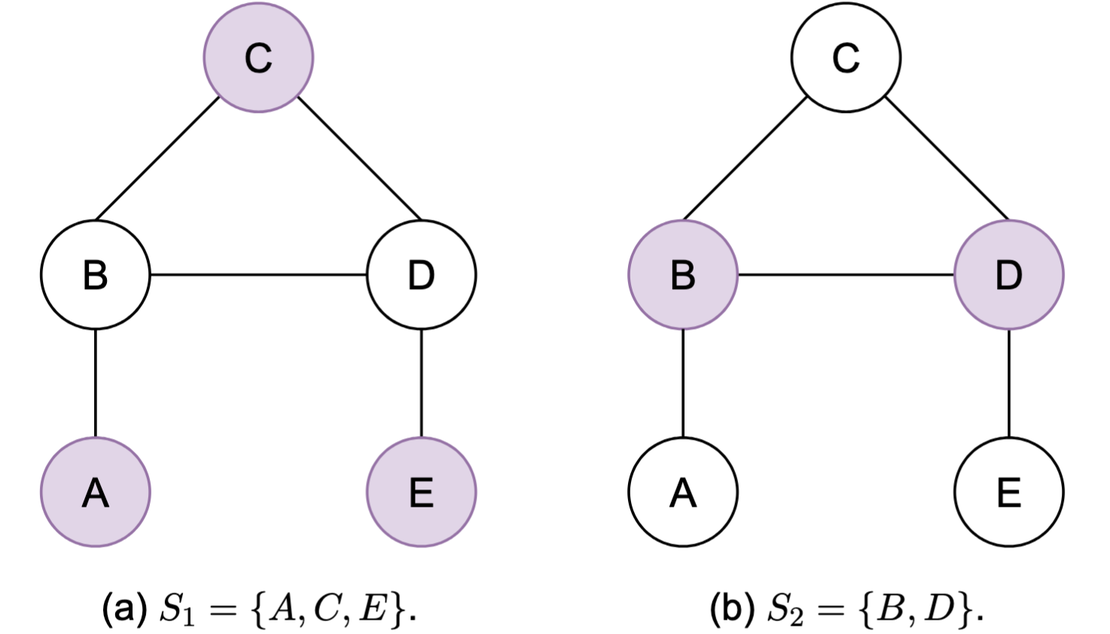
• Minimum Dominating Set: Find the smallest subset of vertices such that every node in the graph is either in the subset or adjacent to a node in it.
• Total Domination Set: Find a subset of vertices such that every node, including those in the subset, has at least one neighbor in the set. Self-domination is not allowed.
• Independent Dominating Set: Find a dominating set that is also an independent set, meaning no two vertices in the set are adjacent.
• Weighted Domination: Each vertex has an associated cost or weight. The goal is to find a dominating set that minimizes the total weight, not necessarily the number of vertices.

Solution Approaches

RedHEUR4.0 promotes the use of some metaheuristics for solving graph domination problems:

• Greedy Randomized Adaptive Search Procedure (GRASP)
• Variable Neighborhood Search (VNS)
• Iterated Greedy (IG)
• Scatter Search (SS)

These are effective tools for tackling complex combinatorial optimization problems, specifically, domination problems. In many real-world situations, metaheuristics provide an efficient alternative capable of delivering high-quality solutions within reduced computation times.

References

1. Duarte, A. (2007). Metaheurísticas.
2. RedHEUR4.0 Proposal. (2022). Red Española de Optimización Heurística 4.0: Digitalización.
3. Wang, F. (2011). On positive influence dominating sets in social networks.

Acknowledgments

Supported by the Spanish Ministry of Science and Innovation, this summary reflects the ongoing work of the RedHEUR4.0 network in promoting research on graph domination problems and their role in the development of advanced optimization techniques.